Identidades Trigonométricas Una identidad trigonométrica es una igualdad entre expresiones que contienen funciones trigonométricas y es válida para todos los valores del ángulo en los que están definidas las funciones (y las operaciones aritméticas involucradas).
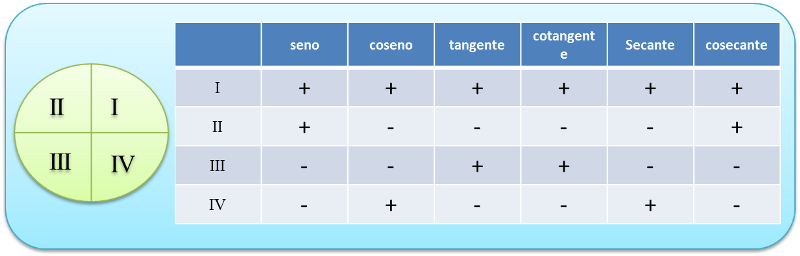
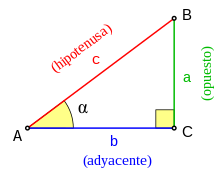
Notación: se define sen2α como (sen α)2. Lo mismo se aplica a las demás funciones trigonométricas.  1) Tg α= Sen α / Cos α = Tangente 2) Ctg α= 1/ Tg α o Ctg α = Cos α / Sen α= Contangente 3) Sec α= 1 / Cos α y por tanto Cos α = 1 / Sen α= Secante 4) Csc α= 1 / sen α y por tanto Sen α= 1 / Csc α= Cosecante 5) Cos 2 α + Sen2 α = 1 6) 1 + Tg 2 α = Sec 2 α 7) Csc2 α = Ctg2 α +1 Ejercicios a) 1 - Sen2α / 1 - Cos2 α = Ctg2 α Cos2 α / Sen2 α = Ctg2 α Ctg2 α = Ctg2 α b) Cos α * Tg α = Sen α Co/s α * Sen α / Co/s α = Sen α Sen α = Sen α
1) Tg α= Sen α / Cos α = Tangente 2) Ctg α= 1/ Tg α o Ctg α = Cos α / Sen α= Contangente 3) Sec α= 1 / Cos α y por tanto Cos α = 1 / Sen α= Secante 4) Csc α= 1 / sen α y por tanto Sen α= 1 / Csc α= Cosecante 5) Cos 2 α + Sen2 α = 1 6) 1 + Tg 2 α = Sec 2 α 7) Csc2 α = Ctg2 α +1 Ejercicios a) 1 - Sen2α / 1 - Cos2 α = Ctg2 α Cos2 α / Sen2 α = Ctg2 α Ctg2 α = Ctg2 α b) Cos α * Tg α = Sen α Co/s α * Sen α / Co/s α = Sen α Sen α = Sen α
 1) Tg α= Sen α / Cos α = Tangente 2) Ctg α= 1/ Tg α o Ctg α = Cos α / Sen α= Contangente 3) Sec α= 1 / Cos α y por tanto Cos α = 1 / Sen α= Secante 4) Csc α= 1 / sen α y por tanto Sen α= 1 / Csc α= Cosecante 5) Cos 2 α + Sen2 α = 1 6) 1 + Tg 2 α = Sec 2 α 7) Csc2 α = Ctg2 α +1 Ejercicios a) 1 - Sen2α / 1 - Cos2 α = Ctg2 α Cos2 α / Sen2 α = Ctg2 α Ctg2 α = Ctg2 α b) Cos α * Tg α = Sen α Co/s α * Sen α / Co/s α = Sen α Sen α = Sen α
1) Tg α= Sen α / Cos α = Tangente 2) Ctg α= 1/ Tg α o Ctg α = Cos α / Sen α= Contangente 3) Sec α= 1 / Cos α y por tanto Cos α = 1 / Sen α= Secante 4) Csc α= 1 / sen α y por tanto Sen α= 1 / Csc α= Cosecante 5) Cos 2 α + Sen2 α = 1 6) 1 + Tg 2 α = Sec 2 α 7) Csc2 α = Ctg2 α +1 Ejercicios a) 1 - Sen2α / 1 - Cos2 α = Ctg2 α Cos2 α / Sen2 α = Ctg2 α Ctg2 α = Ctg2 α b) Cos α * Tg α = Sen α Co/s α * Sen α / Co/s α = Sen α Sen α = Sen α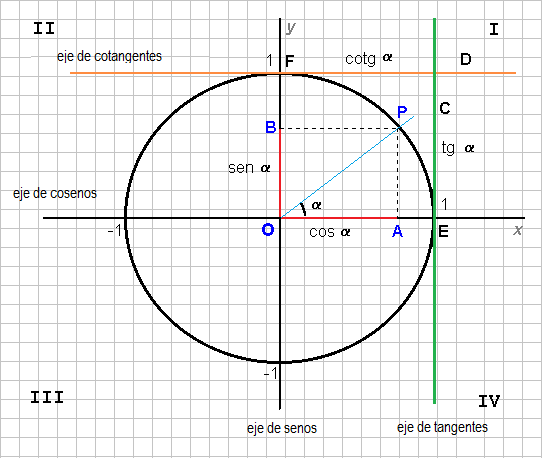






 , correspondiente al vértice A, situado en el centro de la circunferencia.
, correspondiente al vértice A, situado en el centro de la circunferencia.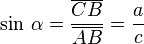
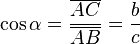












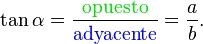
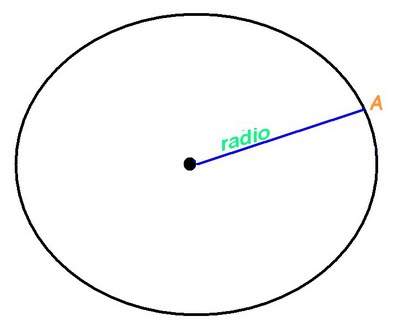 El arco de la circunferencia sera igual al perímetro de la misma cuya formula es (S= P= 2*PI*R.) Entonces la medida en radian sera: (A= S/R= 2*PI*R/R= 2*PI*Rad) Una circunferencia representa un angulo que da un giro completo, por lo que: (360g=2PI*Rad) Es muy usual el uso del sistema radian que el angulo se exprese como múltiplo de PI, e incluso se obvia la unidad rad. En forma análoga el ejemplo anterior, es posible obtener las siguientes equivalencias: 30g= PI/6 45g =PI/4 60g=PI/3 90g=PI/2 180g=PI 360g=2PI Notese que no se utilizo la unidad radian.
El arco de la circunferencia sera igual al perímetro de la misma cuya formula es (S= P= 2*PI*R.) Entonces la medida en radian sera: (A= S/R= 2*PI*R/R= 2*PI*Rad) Una circunferencia representa un angulo que da un giro completo, por lo que: (360g=2PI*Rad) Es muy usual el uso del sistema radian que el angulo se exprese como múltiplo de PI, e incluso se obvia la unidad rad. En forma análoga el ejemplo anterior, es posible obtener las siguientes equivalencias: 30g= PI/6 45g =PI/4 60g=PI/3 90g=PI/2 180g=PI 360g=2PI Notese que no se utilizo la unidad radian.