Circulo Trigonométrico                                       Círculo trigonométrico. También conocido como goniométrico, es aquel círculo cuyo centro coincide con el origen de coordenadas del plano cartesiano y cuyo radio mide la unidad. El círculo trigonométrico tiene la ventaja de ser una herramienta práctica en el manejo de los conceptos de trigonometría, pero al mismo tiempo es un apoyo teórico, pues ayuda a fundamentar y tener una idea precisa y formal de las funciones trigonométricas. Atreves del círculo trigonométrico se puede obtener de forma manual o analítica el valor aproximado de las razones trigonométricas para un ángulo determinado si se dispone de los instrumentos geométricos necesarios. 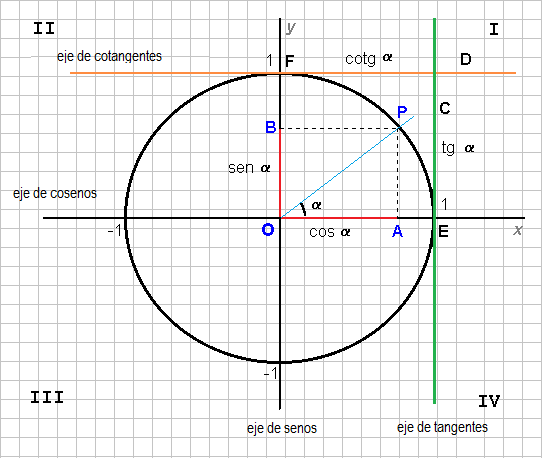                                                                                                                                                                                                                                Coseno de α. Partiendo del ángulo α y la recta r se obtiene un punto P, si se traza una línea perpendicular desde ese punto y hacia el eje X se obtiene un segmento OA que se denomina coseno de α.

Tangente de α. Una línea tangente es la que solo toca en un punto a la circunferencia.

Cotangente de α. Si trazamos una recta FD que sea tangente al punto F y que toque a la recta OD, FD es cotangente de α.

Cuadrantes del Circulo Trigonometrico 

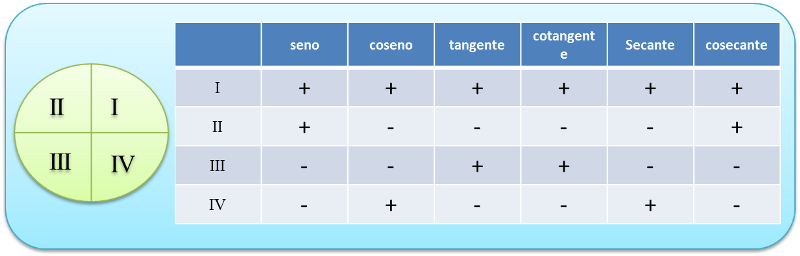
Si dividimos el círculo en 4 partes iguales a cada parte se le conoce como cuadrante, en cada cuadrante las funciones seno, coseno , tangente y cotangente cambian su valor.

Primer cuadrante. Si aumenta el ángulo α disminuye el valor del coseno y  de la cotangente pero aumenta el valor de la tangente y del seno.

Segundo cuadrante. Si aumenta el ángulo α, disminuye el valor del seno, del coseno, de la tangente y de la cotangente.

Tercer cuadrante. Si aumenta el ángulo α, disminuye el valor del seno, del coseno y de la cotangente pero aumenta el valor de la tangente.

Cuarto cuadrante. Si aumenta el ángulo α, disminuye el valor del seno y de la tangente pero aumenta el valor del coseno y de la cotangente.